INTRODUCTION
Resistance elements come in many types conforming to different standards,
capable of different temperature ranges, with various sizes and
accuracies available. But they all function in the same manner: each has
a pre-specified resistance value at a known temperature which changes in a
predictable fashion. In this way, by measuring the resistance of the
element, the temperature of the element can be determined from
tables, calculations or instrumentation. These resistance elements are the
heart of the RTD (Resistance Temperature Detector). Generally, a
bare resistance element is too fragile and sensitive to be used in its raw form,
so it must be protected by incorporating it into an RTD.
Resistance Temperature Detector is a general term for any device that
senses temperature by measuring the change in resistance of a material.
RTD’s come in many forms, but usually appear in sheathed form. An RTD
probe is an assembly composed of a resistance element, a sheath, lead wire
and a termination or connection. The sheath, a closed end tube, immobilizes
the element, protecting it against moisture and the environment to be
measured. The sheath also provides protection and stability to the transition
lead wires from the fragile element wires.
Some RTD probes can be combined
with thermowells for additional
protection. In this type of application,
the thermowell may not only add
protection to the RTD, but will also seal
whatever system the RTD is to
measure (a tank or boiler for instance)
from actual contact with the RTD. This
becomes a great aid in replacing the
RTD without draining the vessel or
system.
Thermocouples are the old tried and
true method of electrical temperature
measurement. They function very
differently from RTD’s but generally
appear in the same configuration: often
sheathed and possibly in a thermowell.
Basically, they operate on the Seebeck
effect, which results in a change in
thermoelectric emf induced by a
change in temperature. Many
applications lend themselves to either
RTD’s or thermocouples.
Thermocouples tend to be more
rugged, free of self-heating errors and
they command a large assortment of
instrumentation. However, RTD’s,
especially platinum RTD’s, are more
stable and accurate.
RESISTANCE ELEMENT CHARACTERISTICS
There are several very important
details that must be specified in order
to properly identify the characteristics
of the RTD:
1. Material of Resistance Element (Platinum, Nickel, etc.)
2. Temperature Coefficient
3. Nominal Resistance
4. Temperature Range of Application
5. Physical Dimensions or Size Restrictions
6. Accuracy
1. Material of Resistance Element
Several metals are quite common for
use in resistance elements and the
purity of the metal affects its
characteristics. Platinum is by far the
most popular due to its linearity with
temperature. Other common materials
are nickel and copper, although most of
these are being replaced by platinum
elements. Other metals used, though
rarely, are Balco (an iron-nickel alloy),
tungsten and iridium.
2.Temperature Coefficient
The temperature coefficient of an
element is a physical and electrical
property of the material. This is a term
that describes the average resistance
change per unit of temperature from ice
point to the boiling point of water.
Different organizations have adopted
different temperature coefficients as
their standard. In 1983, the IEC
(International Electrotechnical
Commission) adopted the DIN
(Deutsche Institute for Normung)
standard of Platinum 100 ohm at 0ºC
with a temperature coefficient of
0.00385 ohms per ohm degree
centigrade. This is now the accepted
standard of the industry in most
countries, although other units are
widely used. A quick explanation of
how the coefficient is derived is as
follows: Resistance at the boiling point
(100ºC) =138.50 ohms. Resistance at
ice point (0ºC) = 100.00 ohms. Divide
the difference (38.5) by 100 degrees
and then divide by the 100 ohm
nominal value of the element. The
result is the mean temperature
coefficient (alpha) of 0.00385 ohms per
ohm per ºC.
Some of the less common materials and temperature coefficients are:
| Pt TC | = | .003902 (U.S. Industrial Standard) |
| Pt TC | = | .003920 (Old U.S. Standard) |
| Pt TC | = | .003923 (SAMA) |
| Pt TC | = | .003916 (JIS) |
| Copper TC | = | .0042 |
Nickel TC | = | 0.00617 (DIN) |
| Nickel TC | = | .00672 (Growing Less Common in U.S.) |
| Balco TC | = | .0052 |
| Tungsten TC | = | 0.0045 |
Please note that the temperature
coefficients are the average values
between 0 and 100ºC. This is not to
say that the resistance vs. temperature
curves are truly linear over the
specified temperature range.
3. Nominal Resistance
Nominal Resistance is the prespecified
resistance value at a given
temperature. Most standards, including
IEC-751, use 0ºC as their reference
point. The IEC standard is 100 ohms at
0ºC, but other nominal resistances,
such as 50, 200, 400, 500, 1000 and
2000 ohm, are available.
4.Temperature Range of Application
Depending on the mechanical
configuration and manufacturing
methods, RTD’s may be used from
-270ºC to 850ºC. Specifications for
temperature range will be different, for
thin film, wire wound and glass
encapsulated types, for example.
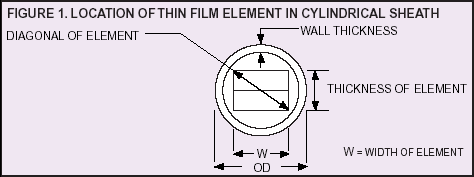
5. Physical Dimensions or Size Restrictions
The most critical dimension of the
element is outside diameter (O.D.),
because the element must often fit
within a protective sheath. The film type
elements have no O.D. dimension.To
calculate an equivalent dimension, we
need to find the diagonal of an end
cross section (this will be the widest
distance across the element as it is
inserted into a sheath).
Permissible deviations from basic values
| Class A |
Temperature
ºC | Deviation |
| ohms | ºC |
| -200 | ±0.24 | ±0.55 |
| -100 | ±0.14 | ±0.35 |
| 0 | ±0.06 | ±0.15 |
| 100 | ±0.13 | ±0.35 |
| 200 | ±0.20 | ±0.55 |
| 300 | ±0.27 | ±0.75 |
| 400 | ±0.33 | ±0.95 |
| 500 | ±0.38 | ±1.15 |
| 600 | ±0.43 | ±1.35 |
| 650 | ±0.46 | ±1.45 |
| |
| Class B |
Temperature
ºC | Deviation |
| ohms | ºC |
| -200 | ±056 | ±1.3 |
| -100 | ±0.32 | ±0.8 |
| 0 | ±0.12 | ±0.3 |
| 100 | ±0.30 | ±0.8 |
| 200 | ±0.48 | ±1.3 |
| 300 | ±0.64 | ±1.8 |
| 400 | ±0.79 | ±2.3 |
| 500 | ±0.93 | ±2.8 |
| 600 | ±1.06 | ±3.3 |
| 650 | ±1.13 | ±3.6 |
| 700 | ±1.17 | ±3.8 |
| 800 | ±1.28 | ±4.3 |
| 850 | ±1.34 | ±4.6 |
|
For example, using an element that is
10 x 2 x 1.5 mm, the diagonal can be
found by taking the square root of (22 +
1.52).Thus, the element will fit into a
2.5 mm (0.98") inside diameter hole. For
practical purposes, remember that any
element 2 mm wide or less will fit into a
1/8" O.D. sheath with 0.010" walls,
generally speaking. Elements which are
1.5 mm wide will typically fit into a
sheath with 0.084" bore. Refer to Figure
1.
6. Accuracy
IEC 751 specifications for Platinum
Resistance Thermometers have
adopted DIN 43760 requirements for
accuracy. DIN-IEC Class A and Class B
elements are shown in the chart on this
page.
7. Response Time
50% Response is the time the
thermometer element needs in order to
reach 50% of its steady state value.
90% Response is defined in a similar
manner. These response times of
elements are given for water flowing
with 0. 2 m/s velocity and air flowing at
1 m/s.They can be calculated for any
other medium with known values of
thermal conductivity. In a 1/4" diameter
sheath immersed in water flowing at
3 feet per second, response time to
63% of a step change in temperature is
less than 5.0 seconds.
8. Measurement Current and Self Heating
Temperature measurement is carried
out almost exclusively with direct
current. Unavoidably, the measuring
current generates heat in the RTD.The
permissible measurement currents are
determined by the location of the
element, the medium which is to be
measured, and the velocity of moving
media. A self-heating factor, “S”, gives
the measurement error for the element
in ºC per milliwatt (mW). With a given
value of measuring current, I, the
milliwatt value P can be calculated from
P = I2R, where R is the RTD’s
resistance value. The temperature
measurement error Δ T (ºC) can then be
calculated from Δ T = P x S.
RESISTANCE ELEMENT SPECIFICATIONS
Stability: Better than 0.2ºC after 10,000 hours at maximum temperature
(1 year, 51 days, 16 hours continuous).
Vibration Resistance: 50 g @ 500ºC; 200 g @ 20ºC; at frequencies from 20 to 1000 cps.
Temperature Shock Resistance: In
forced air: over entire temperature
range. In a water quench: from 200 to
20ºC.
Pressure Sensitivity: Less than 1.5 x
10-4 C/PSI, reversible.
Self Heating Errors & Response Times: Refer to specific Temperature
Handbook pages for the type of
element selected.
Self Inductance From Sensing Current: Can be considered negligible
for thin film elements; typically less than
0.02 microhenry for wire wound
elements.
Capacitance: For wire wound elements:
calculated to be less than 6 PicoFarads;
for film-type elements: capacitance is too
small to be measured and is affected by
lead wire connection. Lead connections
with element may indicate about 300 pF
capacitance.
LEAD WIRE CONFIGURATIONS
As stated previously, a Resistance
Temperature Detector (RTD) element
generally appears in a sheathed form.
Obviously, all of the criteria applicable to
resistance elements also apply here,
but rather than element size, the
construction and dimensions of the
entire RTD assembly must be
considered. Since the lead wire used
between the resistance element and the
measuring instrument has a resistance
itself, we must also supply a means of
compensating for this inaccuracy. Refer
to Figure 2 for the 2-wire configuration.
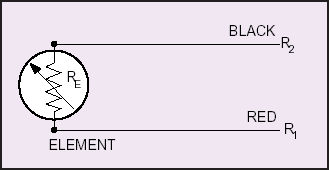
FIGURE 2. 2-WIRE CONFIGURATION (STYLE 1)
The circle represents the resistance
element boundaries to the point of
calibration. 3- or 4-wire configuration
must be extended from the point of
calibration so that all uncalibrated
resistances are compensated.
The resistance RE is taken from the
resistance element and is the value
that will supply us with an accurate
temperature measurement.
Unfortunately, when we take our
resistance measurement, the
instrument will indicate RTOTAL:
Where
RT = R1 + R2 + RE
This will produce a temperature
readout higher than that actually
being measured. Many systems can
be calibrated to eliminate this. Most
RTD’s incorporate a third wire with
resistance R3. This wire will be
connected to one side of the
resistance element along with lead
2 as shown in Figure 3.
This configuration provides one
connection to one end and two to
the other end of the sensor.
Connected to an instrument
designed to accept 3-wire input,
compensation is achieved for lead
resistance and temperature change
in lead resistance. This is the most
commonly used configuration.
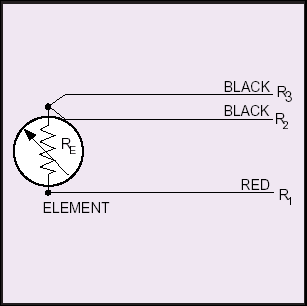
FIGURE 3. 3-WIRE CONFIGURATION (STYLE 2)
If three identical type wires are used
and their lengths are equal, then R1
= R2 = R3. By measuring the
resistance through leads 1, 2 and
the resistance element, a total
system resistance is measured (R1
+ R2 + RE ). If the resistance is also
measured through leads 2 and 3 (R2
+ R3), we obtain the resistance of
just the lead wires, and since all
lead wire resistances are equal,
subtracting this value (R2 + R3) from
the total system resistance (R1 + R2
+ RE) leaves us with just RE, and an
accurate temperature measurement
has been made. A 4-wire
configuration is also used. (See
Figure 4.) Two connections are provided to each end of the sensor.
This construction is used for
measurements of the highest
precision.
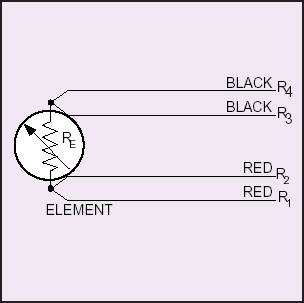
FIGURE 4. 4-WIRE CONFIGURATION (STYLE 3)
With the 4-wire configuration, the
instrument will pass a constant
current (I) through the outer leads, 1
and 4.
The voltage drop is measured
across the inner leads, 2 and 3. So
from V = IR we learn the resistance
of the element alone, with no effect
from the lead wire resistance. This
offers an advantage over 3-wire
configurations only if dissimilar lead
wires are used, and this is rarely the case.
Still another configuration, now rare,
is a standard 2-wire configuration
with a closed loop of wire alongside
(Figure 5). This functions the same
as the 3-wire configuration, but uses
an extra wire to do so. A separate
pair of wires is provided as a loop to
provide compensation for lead
resistance and ambient changes in
lead resistance.
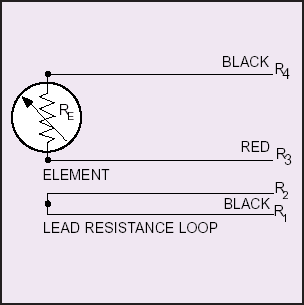
FIGURE 5. 2-WIRE CONFIGURATION PLUS LOOP (STYLE 4)
|
